Mon message au sujet de voir un laser de la lune mentionné le fait que le faisceau laser se propage à partir d'une mesure qu'il se propage. Nous sommes habitués à voir ce à partir d'une lampe de poche - le faisceau d'une lampe de poche dans une pièce est beaucoup plus petit que le faisceau d'une lampe de poche asross un champ ouvert. Les lasers sont répandues trop, mais pas autant. Mais ils le font répandre, et plus du quart de un million de miles de la lune, un laser se propage un peu. La propagation d'un laser (qui est plus acurately appelé sa divergence angulaire) peut être réduite mais, ce qui est utile si vous voulez que votre diamètre du faisceau à être plus petits sur de longues distances. Les limites de ce procédé sont la peine de parler.
Commençons avec le cas le plus simple d'une loupe est utilisé pour allumer un feu. Il prend un objet comme le soleil, et produit une image minuscule mais intense du soleil sur la cible que vous essayez de mettre le feu. Pour l'imagerie générale, la distance par rapport à S1 objet et la distance à l'image S2 sont liés à la distance focale f de la lentille.


Le grossissement de la lentille est donnée par

Voici le grossissement est de grossissement linéaire. Le soleil est gigantesque, l'image du soleil créé par la loupe est une petite piqûre de lumière brillante. Par conséquent, le grossissement est en fait incroyablement petit. Nous pouvons mettre des chiffres de l'en supposant que le soleil est très loin par rapport à la distance focale (c'est à dire, que 1/s1 est essentiellement 0 contre 1 / f.), Et en écrivant la taille du soleil, comme θ * s1 , où θ est la taille angulaire du Soleil (environ un demi-degré).
Faire tout cela, et vous verrez que la taille de l'image focalisée du soleil (appelons-d) est la suivante:

Le signe moins signifie simplement que l'image est à l'envers. Pour une loupe avec une longueur focale de 15 cm, la lumière qui pénètre dans la loupe est concentrée en une image du soleil seulement 0,13 centimètres de diamètre. Distances focales plus courtes signifient des images plus petites et plus de concentration de la lumière.
Le résultat de tout ceci est que la focalisation implique des compromis. Si vous voulez une taille de spot plus petit et plus intense au foyer, vous devez vous concentrer plus difficile - la lumière provenant de la loupe doit être dirigé vers le foyer à un angle très pointu. Cet angle par rapport à la taille à la mise au point chose est ce qui finit par être le facteur limitant de la divergence du faisceau laser trop.
Alors jetez un oeil à ce schéma de Wikipedia illustrant un faisceau laser étant focalisé:

Le faisceau a un angle de divergence Θ, et il a une taille minimale de taille w 0 à la mise au point. Sont les deux liés par des faisceaux laser, comme ils le sont pour les images? Oui, en effet. Il s'avère que les deux sont liés par
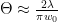 .
.
Où thêta est la longueur d'onde de la lumière. Depuis la longueur d'onde de la lumière visible est très faible, la lumière laser peut être focalisé vers le bas pour des tailles de tache vraiment minuscules résultant de l'intensité des ridicules.
Maintenant, pour le cas de l'envoi d'un faisceau laser sur la lune, nous essayons de réduire l'angle de divergence. Cela signifie que nous avons besoin d'augmenter la taille du faisceau dans la mesure du possible. Cela se fait généralement par l'envoi du laser à travers un télescope. Si le télescope a un diamètre de 1 mètre et vous arranger pour que le faisceau laser d'être élargi pour que la taille à la sortie du télescope, la divergence du faisceau peut en principe être réduit à quelque chose de l'ordre de quelques millièmes de cent-un diplôme. Un tel faisceau aurait seulement augmenté d'environ quelques centaines de mètres au moment où il est arrivé à la lune. Alors que ce n'est pas une petite zone, il suffit d'expériences telles que le calendrier lunaire Apollo allant expériences.
(Note personnelle:..! Désolé pour disparaître de l'internet au cours des deux dernières semaines, j'ai eu mes ronde préliminaire la semaine dernière, et le blog a dû attendre Sur le plan positif, je suis passé sans aucun problème et je suis officiellement All But Dissertation)
Commençons avec le cas le plus simple d'une loupe est utilisé pour allumer un feu. Il prend un objet comme le soleil, et produit une image minuscule mais intense du soleil sur la cible que vous essayez de mettre le feu. Pour l'imagerie générale, la distance par rapport à S1 objet et la distance à l'image S2 sont liés à la distance focale f de la lentille.

Le grossissement de la lentille est donnée par
Voici le grossissement est de grossissement linéaire. Le soleil est gigantesque, l'image du soleil créé par la loupe est une petite piqûre de lumière brillante. Par conséquent, le grossissement est en fait incroyablement petit. Nous pouvons mettre des chiffres de l'en supposant que le soleil est très loin par rapport à la distance focale (c'est à dire, que 1/s1 est essentiellement 0 contre 1 / f.), Et en écrivant la taille du soleil, comme θ * s1 , où θ est la taille angulaire du Soleil (environ un demi-degré).
Faire tout cela, et vous verrez que la taille de l'image focalisée du soleil (appelons-d) est la suivante:
Le signe moins signifie simplement que l'image est à l'envers. Pour une loupe avec une longueur focale de 15 cm, la lumière qui pénètre dans la loupe est concentrée en une image du soleil seulement 0,13 centimètres de diamètre. Distances focales plus courtes signifient des images plus petites et plus de concentration de la lumière.
Le résultat de tout ceci est que la focalisation implique des compromis. Si vous voulez une taille de spot plus petit et plus intense au foyer, vous devez vous concentrer plus difficile - la lumière provenant de la loupe doit être dirigé vers le foyer à un angle très pointu. Cet angle par rapport à la taille à la mise au point chose est ce qui finit par être le facteur limitant de la divergence du faisceau laser trop.
Alors jetez un oeil à ce schéma de Wikipedia illustrant un faisceau laser étant focalisé:

Le faisceau a un angle de divergence Θ, et il a une taille minimale de taille w 0 à la mise au point. Sont les deux liés par des faisceaux laser, comme ils le sont pour les images? Oui, en effet. Il s'avère que les deux sont liés par
Où thêta est la longueur d'onde de la lumière. Depuis la longueur d'onde de la lumière visible est très faible, la lumière laser peut être focalisé vers le bas pour des tailles de tache vraiment minuscules résultant de l'intensité des ridicules.
Maintenant, pour le cas de l'envoi d'un faisceau laser sur la lune, nous essayons de réduire l'angle de divergence. Cela signifie que nous avons besoin d'augmenter la taille du faisceau dans la mesure du possible. Cela se fait généralement par l'envoi du laser à travers un télescope. Si le télescope a un diamètre de 1 mètre et vous arranger pour que le faisceau laser d'être élargi pour que la taille à la sortie du télescope, la divergence du faisceau peut en principe être réduit à quelque chose de l'ordre de quelques millièmes de cent-un diplôme. Un tel faisceau aurait seulement augmenté d'environ quelques centaines de mètres au moment où il est arrivé à la lune. Alors que ce n'est pas une petite zone, il suffit d'expériences telles que le calendrier lunaire Apollo allant expériences.
(Note personnelle:..! Désolé pour disparaître de l'internet au cours des deux dernières semaines, j'ai eu mes ronde préliminaire la semaine dernière, et le blog a dû attendre Sur le plan positif, je suis passé sans aucun problème et je suis officiellement All But Dissertation)
Aucun commentaire:
Enregistrer un commentaire
Nous vous invitons ici à donner votre point de vue, vos informations, vos arguments. Nous refusons les messages haineux, diffamatoires, racistes ou xénophobes, les menaces, incitations à la violence ou autres injures. Merci de garder un ton respectueux et de penser que de nombreuses personnes vous lisent.
La rédaction